等差数列的前n项和
课 题:等差数列的前n项和
教材分析:本节课主要研究如何应用倒序相加法求等差数列的前n项和以及该求和公式的应 用.等差数列在现实生活中比较常见,因此等差数列求和就成为我们在实际生活中经常遇到 的一类问题.同时,求数列前n项和也是数列研究的基本问题,通过对公式的推导,可以让 学生进一步掌握从特殊到一般的研究问题的方法.
学情分析:在本节课之前学生已经学习了等差数列的通项公式及基本性质,这就为倒序相加法的学习提供了基础;同时学生已经学习了二次函数的有关知识,因此在教学中可适当渗透函数思想.高斯的算法与一般等差数列的求和还有一定的距离,如何从首尾配对法引出倒序相加法,这是学生学习的障碍.
设计思想:教学过程中,从介绍高斯的算法开始,探究这种方法如何推广到一般等差数列前n项和的求法.通过设计一些从简单到复杂,从特殊到一般的问题,组织和启发学生获得公式的推导思路,并且充分引导学生展开自主、合作、探究学习,通过生生互动和师生互动形式,让学生在问题解决中学会思考、学会学习. 同时为了促进成 绩优秀学生的发展,我还设计了选做题和探索题,进一步培养优秀生用函数观点分析、解决问题的能力,达到了分层教学的目的.
教学目标:
1.理解等差数列前n 项和公式的推导过程; 掌握并能熟练运用等差数列前 n 项和公式;了解倒序相加法原理.
2.通过公式的推导过程,让学生 验从特殊到一般的研究方法,渗透函数思想与方程思想,培养学生观察、归 纳、反思的能力;通过小组讨论学习,培养学生合作交流和自主探 究的能力.
重点和难点:
重点:探索并掌等差数列前n项和公式,学会用公式解决一些实际问题.
难点:等差数列前n项和公式推导思路的获得.
教学过程:
(一) 创设情景
唤起学生知识经验的感悟和体验世界七大奇迹之一的泰姬陵坐落于印度古都阿格,传说陵寝中有一个三角形图案,以相同大小的圆宝石镶饰而成,共有100层,你 知道这个图案一共花了多少宝石吗?
[知识链接]
高斯,德国著名数学家,被誉为“数学王子”. 200多年前,高斯的算术教师提出了下面的 问题: 1 + 2 + 3 + … +1 0 0 = ?
据说,当其他同学忙于把100个数逐项相加时,10岁的高斯却用下面的方法迅速算出了正确答案:
(1 + 100 ) + (2 + 99 ) + ·… ··+ (50 + 51 ) = 101 ×5 0 = 5 0 5 0.
[学情预设] 高斯的算法蕴涵着推导等差数列前n项和的方法——倒序相加法. 教学时,应 给学生提供充裕的时间,让学生们自己去观察、探究、发现和交流它们的内在规律.为了使 学生对这种算法有进一步的理解,我又设计了以下三道由易到难的问题.
(二)由易到难。在自主探究与合作中学习
问题1图案中,第1层到第51层一共有多少颗宝石?
该题组织学生分组讨论,在合作中学习,并把小组发现的方法一一呈现.
[学情预设] 学生可能出现以下求法:
方法1:原式= (1 + 2 + 3 + … … + 50) + 5 1.
方法2:原式 =0 + 1 + 2 + … … + 50 + 5 1.
方法3:原式 = (1 + 2 + … + 25 + 27… + 5 1) + 26.
以上方法实际上是用了“化归思想 ”,将奇数个项问题转化为偶数个项求解,教师应进行充 分肯定表扬.
[设计意图] 这是求奇数个项的和的问题,若简单地摹仿高斯算法,将出现不能全部配对的问题,借此渗透化归思想。
问题2:求图案中从第层到第n 层 (1 < n < 100 ,n ∈N ) 共有多少颗宝石?
[学情预设] 学生通过激烈的讨论后,发现n为奇数时不能配对,可能会分n为奇数、偶数的情况分别求解,教师如何引导学生避免讨论成为该环节的关键.
[设计意图] 从求确定的前n个正整数之和到求一般项数的前n个正整数之和,让学生领会 从特殊到一般的研究方法,旨在让学生对“首尾配对求和”这一算法的改进.
启发:(多媒体演示) 如右图,在三角形图案右侧倒放一个全等的三角形与原图补成平行四边形.
[设计意图] 借助几何图形的直观性,能启迪思路,唤醒学生记忆深处的东西,并为倒序相加法的出现提供了一个直接的模型.
通过以上启发学生再自主探究,相信容易得出解法:
∵1 + 2 + 3 + … + (n-1)+n;
n + (n-1) + (n-2 ) +…+ 2 + 1;
∴(n + 1) + (n + 1) + (n + 1) + …;
∴1 + 2 + 3 + … + n=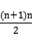
问题3: 在公差为d的等差数列{an }中,定义前n项和
Sn=a1+ a2 + … +a n,如何求Sn?
组织学生讨论:
在公式中若将an=a1 + (n-1) d 代人又可得出哪个表达式?
讲授新课
1.等差数列的前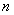 项和公式1:
项和公式1: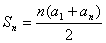
证明: 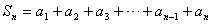 ①
①
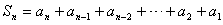 ②
②
①+②: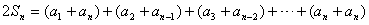
∵
∴ 由此得:
由此得: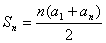
从而我们可以验证高斯十岁时计算上述问题的正确性
2. 等差数列的前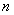 项和公式2:
项和公式2: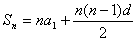
用上述公式要求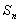 必须具备三个条件:
必须具备三个条件: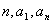
但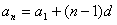 代入公式1即得:
代入公式1即得: 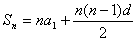
此公式要求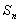 必须已知三个条件:
必须已知三个条件: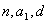 (有时比较有用)
(有时比较有用)
[范例讲解]
课本P49-50的例1、例2、例3
由例3得与 之间的关系:
之间的关系:
由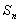 的定义可知,当n=1时,
的定义可知,当n=1时,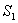 =
=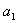 ;当n≥2时,
;当n≥2时, =
=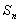 -
-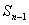 ,
,
即 =
=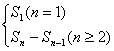 .
.
课堂练习
课本P52练习1、2、3、4
课时小结
本节课学习了以下内容:
1.等差数列的前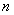 项和公式1:
项和公式1: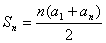
2.等差数列的前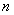 项和公式2:
项和公式2: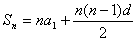
课后作业
课本P52-53习题[A组]2、3题
教学反思:
“等差数列前n项和”的推导不只一种方法,本节课是通过介绍高斯的算法,探究这种 方法如何推广到一般等差数列的求和.该方法反映了等差数列的本质,可以进一步促进学生 对等差数列性质的理解.本节课教学过程的难点在于如何获得推导公式的“倒序相加法”这一思路.为了突破这一难点,在教学中采用了以问题驱动的教学方法,设计的三个问题体现 了分析、解决问题的一般思路,即从特殊问题的解决中提炼方法,再试图运用这一方法解决一般问题. 在教学过程中,通过教师的层层引导、学生的合作学习与自主探究,学生“倒序相加法”思路的获得就水到渠成了.https://math.sqnu.edu.cn/sfrz/zc
